
L’Histoire de la bourse retiendra les fardeaux lourds et épuisant ayant accablé la cote de la bourse et les dégâts qu’ils ont causé au marché et aux épargnants de bon père de famille, exhortant la BVMT à leur créer un terrain de jeu qui leur est spécialement réservé (une poubelle pour la charognards). Des investissements qui se sont totalement évaporés dans des sociétés introduites à la cote de la bourse dans l’espoir de renforcer leur capacité de création de richesse et leur pérennité. Malencontreusement pour certaines entreprises, certainement de bonne fois parfois (involontairement) mais d’égotisme et de mauvaise gestion dans d’autres cas, ont cumulé des pertes dépassant la totalité de leur fonds propres au moments de leur introduction en bourse. Nous retenons un échantillon d’entreprises privées dont le rendement de leurs cours est en dessous de -80% depuis leur introduction en bourse.

Ces critères nous font ressortir un échantillon de 7 valeurs, dont quatre relèvent du marché principal, à savoir STIP, ELECTROSTAR, GIF-Filter et UADH. Cette dernière c’es introduite au marché principal au moment où le (Ex) marché alternatif existe. Elle est la seule, d’ailleurs, à ne pas encore publier ses comptes de l’exercice 2018, sur cet échantillon.

Tous ces titres ont réalisé un rendement (arithmétique moins que -80%). L’action MIP cumule une variation de -95,5%, malgré que le titre ait enregistré en 2021 YTD (30 septembre) une performance positive de 50%. Pourquoi un titre qui empoche sur une année 50% mais traine une performance globale de -95,5%. Bien entendu ceci est en relation avec la conception mathématique intrinsèque à la méthode de calcul des rendements arithmétiques.
Ce type de rendement ne dégage jamais une performance négative (sur des observations de cours positives) strictement inférieur à -100%.
Par exemple un détenteur d’une action dont le cours passe de 100 à 1, subit une baisse de -99,0%. Mais rien n’empêche que sur la valeur actuelle de 1 dinars, il peut encore réaliser une performance négative de -99%, si le cours passe à 0,01, et ainsi de suite. En tous, l’investisseur a réalisé deux fois une performance sur son titre de -99%, mais cela ne veut pas dire qu’il a cumulé un rendement égal à la somme des deux (-99% + -99% = -198%). Les rendements arithmétiques ne sont pas additifs. L’investisseur a tout simplement réalisé une performance entre 100 et 0,01, soit -99,99%. Pour remonter de 0,01 à 100, il doit réaliser une performance de 999 900%.

Or, avec la méthode de rendement logarithmique (Ln), l’investisseur a réalisé deux fois une performance de -460,5% soit au total (rendements additifs), une perte de -921%. C’est exactement ce qu’il lui faut en positif pour revenir de 0,01 à 100.
Un autre exemple plus simple, en supposant qu’un investisseur détient une action dont le cours est passé de 100 à 50, en t1 puis de 50 à 100 en t2.
En t1 il réalise une performance de -50%, mais pour revenir de 50 à 100, il a réalisé une performance de 100%. Ni la somme des deux rendement en t1 et t2 (50%) ni la moyenne (25%) ne donne le vrai rendement global réalisé in fine qui est de 0% (puisqu’il part de 100 et il revient à 100). Le même investisseur a réalisé en rendement logarithmique -69,3% en t1 et +69,3% en t2, la somme étant 0 ce qui correspond au rendement effectif sur l’ensemble des deux périodes.

Ainsi, pour revenir à sa mise initial, l’investisseur sait pertinemment qu’il doit réaliser un rendement égal à l’opposé du rendement logarithmique enregistré jusque-là.
En d’autres termes, celui qui a acheté MIP à l’IPO à 4,7 dinars et avec un cours actuel de 0,21, soit une perte de -95,5%. Pour revenir à son équilibre, l’action MIP doit remonter (en arithmétique) de 2138,1%
Formulation mathématique et application des rendements logarithmique
La gestion des portefeuilles d’actifs s’appuie sur la notion de rendement ou de taux de rentabilité. Cette grandeur mesure, pendant un intervalle de temps donné, l’appréciation ou la dépréciation relative de la valeur d’un actif financier ou d’un portefeuille d’actifs.
Pour une action et pour une période donnée, on définit usuellement deux types de rendement d’un actif financier Ai de type action :
- Le rendement arithmétique comme la variation relative de son prix Pi (t) entre les instants t et t − 1 donnée par :

- Le rendement logarithmique, également appelé rendement géométrique, entre les instants t et t − 1 est donné par :
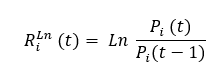
L’inconvénient du rendement arithmétique est qu’il n’est pas additif. En effet, son calcul privilégie les deux instants t et t − 1, et néglige ainsi l’évolution de la valeur pendant la période qui les sépare l’un de l’autre.
Il est à noter que chacun de ces rendements possède son intérêt propre. En effet, l’agrégation temporelle des rendements plaide pour les rendements géométriques. Il est possible de calculer la somme des rendements logarithmiques qui donne le résultat effectivement réalisé sur toute la période, étant donné que les rendements logarithmiques sont additifs.
Le rendement géométrique sur une période est la moyenne des rendements géométriques des n sous périodes. Cette propriété n’est pas vérifiée pour les rendements arithmétiques.
Pour une meilleure appréciation des performances du panier de notre échantillon, l’application des rendements logarithmiques (par opposition aux rendements arithmétiques, les rendements logarithmiques sont symétriques entre la hausse et la baisse, et sont plus adaptés à des valeurs petites) affichent les rendements suivants :

Et dire que des valeurs comme Land ’or, Cerealis et New Body Line ont été introduites au marché alternatif.
Par Moez Hadidane
